




This appendix contains the first chapter of Hooktheory I

Many things in this world couldn’t exist without an important fundamental building block. For living organisms, it is the cell; for skyscrapers, it is the steel I-beam; for modern electronics, it is the transistor. For popular music, it is a set of seven notes called the major scale.
The major scale is just a group of notes that follow a special pattern - one that humans happen to really love. In fact, we love these notes so much that the vast majority of the songs you hear on the radio are built using just these seven notes played in a unique sequence. Doesn’t that seem remarkable?
One set of these notes corresponds to the white keys on the piano. To hear them, click the play button.
Before you criticize this particular ordering of notes as uninteresting and not very musical, know that listening to them in this order is the equivalent of looking at an I-beam sitting on a construction site. However, when re-ordered, these seven notes can create almost every song you know and love. In other words, the white keys of the piano are all you need. Let’s listen to a few:
To be clear, there is nothing special about these specific songs that makes this possible; they were chosen simply because they are iconic and recognizable.
The first note in the scale we just showed you happened to be C, but a major scale can actually be played starting from any note on the piano. Other major scales make use of the black keys, but they all sound basically the same, and any one of them can play all the songs you just heard.
The fact that a major scale can start on any note is the reason songs are said to be written in a “key” like C or F or G - the key indicates the starting note of the scale that the song uses. For example, every song in the medley you just heard used the notes from the C major scale (since the starting note of the scale was C), so they are said to be played in the key of C. The original recordings of these songs don’t all use this particular major scale, but I bet you couldn’t tell and didn’t care; you still heard each song just as you remembered it.
The fact that a major scale can start on any note is convenient for singers because it allows them to sing songs in the key that is most comfortable for their vocal range, but it makes trying to understand music a real mess. Consider two frequently used major scales: C major and D major:

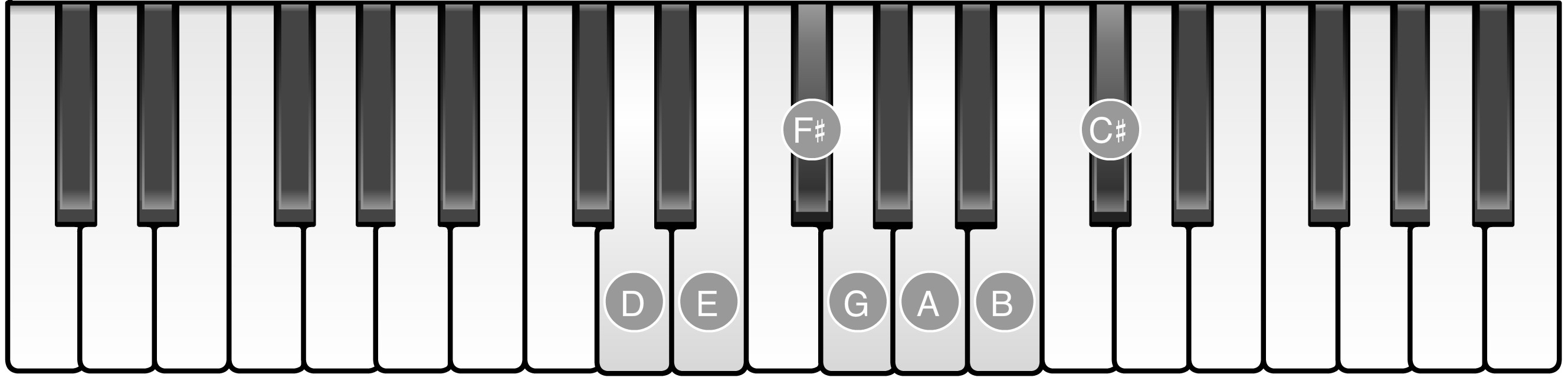
Notice that the note D shows up in both scales. The note D, however, is in a different position in each scale: it’s the second note in the C major scale and the first note in the D major scale.
This is important because the way a note is used in a song is determined by its position in the scale rather than its letter name. D plays a completely different role in a song written in C major than a song written in D major.
Trying to understand a song by looking at just the names of the notes it contains isn’t very useful because it ignores this fundamental fact. Fortunately, there is a simple solution that makes understanding the structure of a melody and comparing different songs straightforward.
So far, you have learned that:
1. the lettered names of the notes contained in a song are of no help for understanding what is going on unless they are considered in the context of the major scale that a song is using.
2. the particular major scale that a song happens to use doesn’t matter. Most songs can be played entirely with the white keys of the piano (the C major scale), but they wouldn’t sound much different if they were played in some other major scale that makes use of a different set of notes.
For these reasons, it’s easier and more intuitive to understand music by referring to notes in a song by their position in their scale (1-7) rather than their actual letter names (C, D, E, ..., for example). To introduce you to this notation, often called relative notation, consider the two major scales you saw before but now marked up with numbered labels and colors to emphasize each note’s position in the major scale.
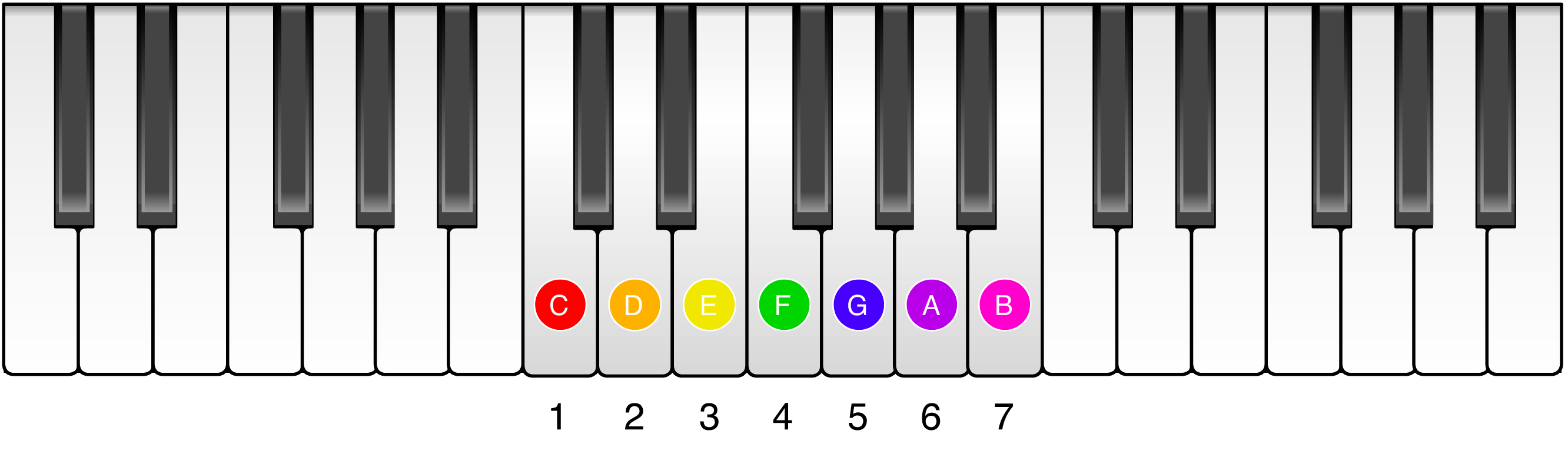
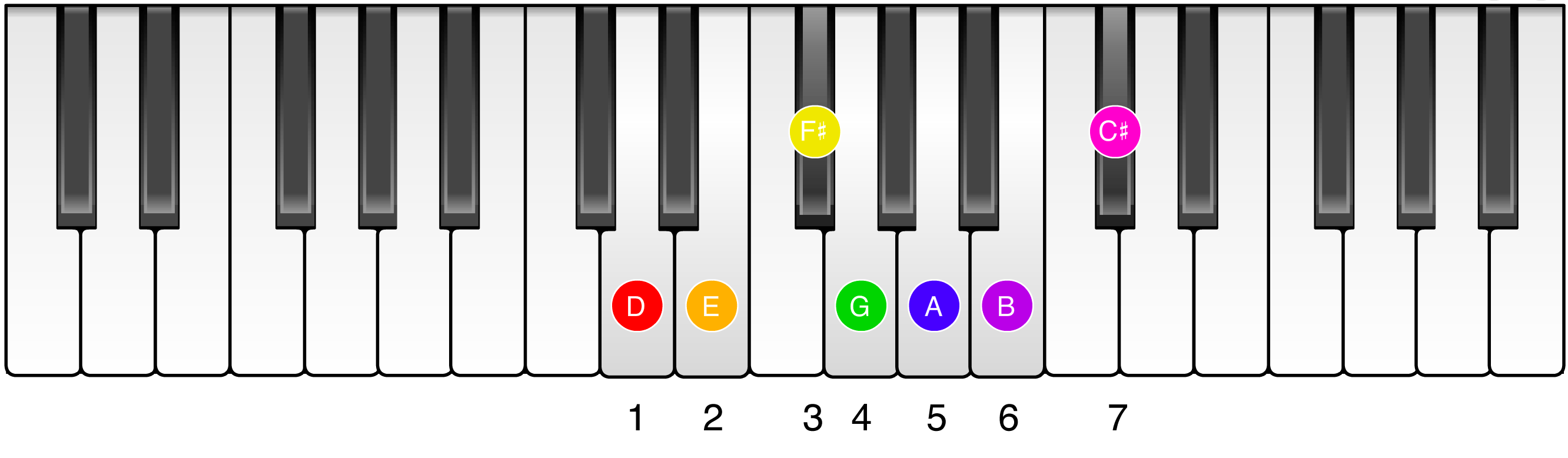
When notes are referred to by their position in a scale, they are referred to as scale degrees. The note D, for example, is scale degree 2 of the C major scale since it is the second note of the C major scale, but it’s scale degree 1 of the D major scale.
One of the most useful things about relative notation is that it enables songs that use scales with different starting notes to be compared side-by-side. For instance, one can compare a sequence of scale degrees rather than two different sets of lettered notes.
Since relative notation makes it easier to learn music, we created a simple way to display music in relative notation. The next example shows the C major scale displayed in relative notation on a staff. Each colored rectangle corresponds to a note. The vertical position indicates its scale degree (1, 2, 3, etc.) instead of its note name (C, D, E, etc). Color is used as an additional visual indicator of each scale degree. Red, for example, is always scale degree 1 regardless of the scale a song is using. Green corresponds to scale degree 4. The length of each note indicates its duration. When you click play, you will hear the scale degrees of the C major scale:
The next example shows the G major scale on the relative staff. Notice that even though the C major scale and the G major scale are different on the piano, they look identical on the relative staff since both use the exact same scale degrees as they play (1-2-3-4-5-6-7-1).
In the previous examples, the fourth scale degree of the C major scale happens to be F. In the G major scale, it happens to be a C. In the relative system, however, both notes are represented by a green scale degree 4 to emphasize their sameness.
A major scale is very simple, and you might be asking how this works with actual songs. Since most songs only use notes from the major scale, they can be represented naturally with relative notation regardless of the key they are written in. Below is the melody from the chorus of “Livin’ On A Prayer” by Bon Jovi visualized with the relative staff.
Thinking about melodies as numbers representing positions in a scale makes it much easier to compare different melodies at a glance. It also makes it easier to analyze and understand melodies because the position of the note in the scale is what determines function rather than the actual note name itself.
The melody from “Livin’ On A Prayer” uses scale degrees 1-1-1-7-6-5-3-4-4-... in succession. If the song happened to use the C major scale, these scale degrees would correspond to the notes C-C-C-B-A-G-E-F-F, but it could just as well have been written in G major where these scale degrees would correspond to entirely different notes (G-G-G-F#-E-D-B-C-C).
When we study the melodies and chords of different songs to look for patterns, we want to compare apples to apples, so the note names just won’t do.
In the previous section you were introduced to the idea of understanding the notes in a song’s melody using a relative system. However, songs usually have many other notes being played besides the melody. These other notes work together to create rich sounds called chords. In this section we will extend the concept of relative notation to chords and learn how to break up a song into its two basic building blocks: its melody and its chords.
Just as with the notes in the melody, the notes that form the chords of a song typically limit themselves to the same seven notes of whichever major scale the song happens to use. To give a specific example, there are lots of possible chords in music, but if a song is written in C, you are likely to find that it only uses chords that can be formed using the white keys of the piano.
Because there are only seven notes in the major scale, there end up being only seven basic chords that can show up in a given song. Just as we did with melody, labeling these seven possible chords with numbers turns out to be very useful. The first of these chords is built off the first scale degree and for this reason is called the I (“one”) chord.
Since we will now be using numbers to refer to both chords and notes, to avoid confusion, we will use italicized Roman numerals when referring to chords.
In addition to using scale degree 1, the I chord also contains the scale degrees 3, and 5. In the key of C, this corresponds to the notes C, E, and G and creates a C major chord. Let’s listen to scale degrees 1, 3, and 5 of the C major scale. First we will play each scale degree individually, then we will play scale degrees 1, 3, and 5 (notes C, E, and G) at the same time to create a I chord.
Now you may be thinking that a simple chord like this with only three notes couldn’t possibly be very useful. After all, songs certainly aren’t limited to playing just three notes at once!
It turns out the I chord need not be played with scale degrees 1, 3, and 5 arranged exactly as we just showed you; as long as scale degree 1 is the lowest note, you can reorder the other scale degrees and play any of them more than once. The next example shows a few variations of scale degrees 1, 3, and 5 that also form I chords.
This means that even if it looks like a chord has a lot of notes in it, it’s often likely still just playing three distinct scale degrees corresponding to one of the basic chords.
We’ve been showing you a lot of pianos, but this all works the same way regardless of instrument. If you put your fingers on the following frets of a guitar and strum, the strings will play the labeled notes, also resulting in a I chord in the key of C:
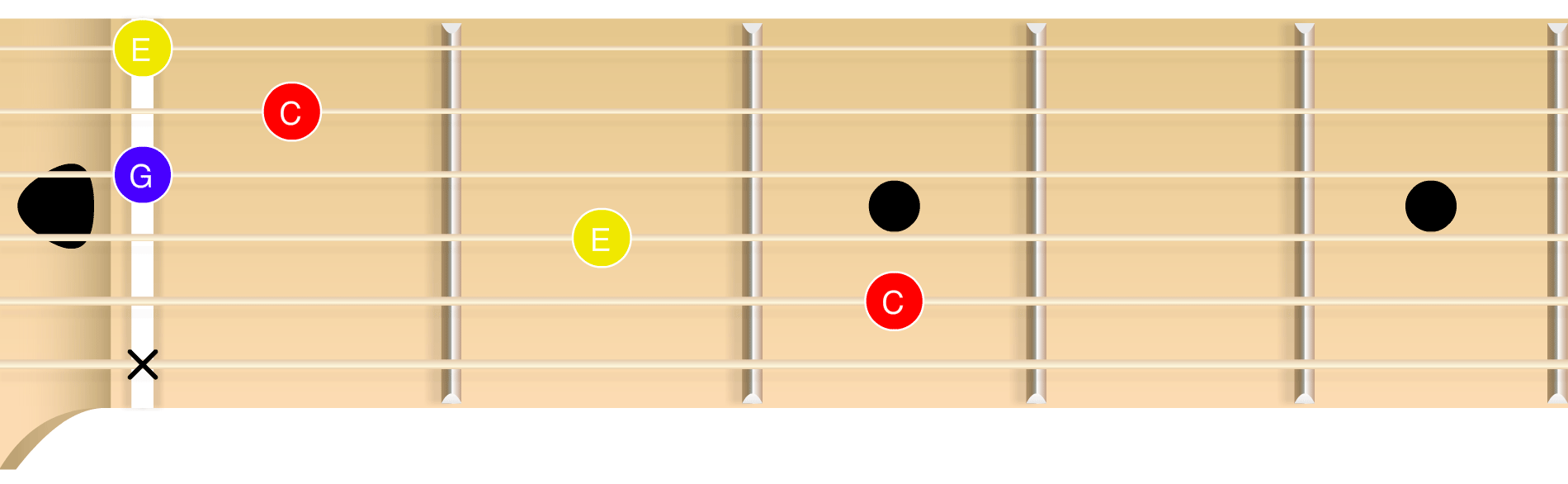
Note that even though five strings are played, only three distinct scale degrees are involved: 1, 3, and 5 of the C major scale. Scale degrees 1 and 3 (red, and yellow) are repeated twice. The majority of standard chords on guitar play all six strings yet only involve three distinct notes.
The other six basic chords are built just like the I chord. The ii chord (“two” chord) is built from scale degree 2 of the major scale and contains scale degrees 2, 4, and 6. Let’s listen to scale degrees 2, 4, and 6 of a major scale starting on the note C. First we will play each scale degree individually, then we will play scale degrees 2, 4, and 6 at the same time to create a ii chord.
In the key of C, the ii chord corresponds to a D minor chord. Minor chords have a different sound than major chords (the I chord you heard before is a major chord). The reason for this turns out to be a difference in the relative spacing between the scale degrees that make up the chords. In the next graphic, we illustrate this on the piano by counting the notes between scale degrees 1 and 3 in the key of C (notes C and E), and comparing it to the number of notes between scale degrees 2 and 4 in the key of C (notes D and F). This spacing difference between the scale degrees that make up each chord causes the chords to have a different sound.
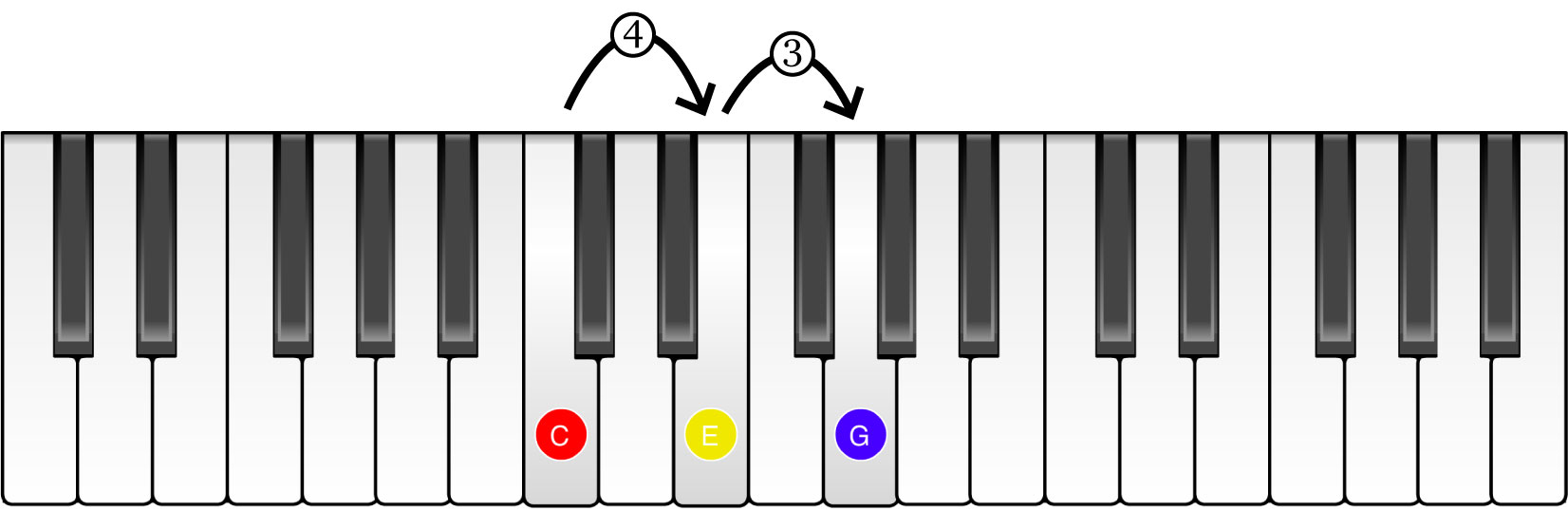
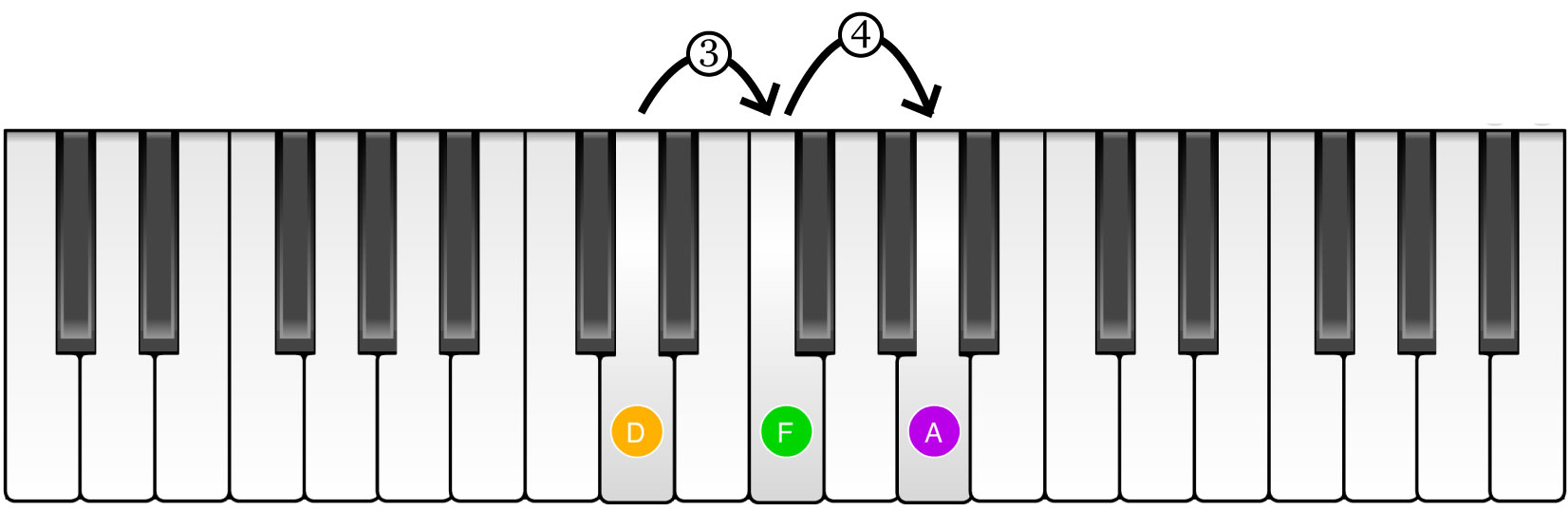
When people compare the sounds of major and minor chords, they often say minor chords sound more dissonant and “somber”, while major chords are more “bright” sounding.
To make it immediately obvious whether a chord has a minor quality or a major quality, we use upper case Roman numerals for major chords and lower case Roman numerals for minor chords. This means that we’ll always refer to the second chord as a ii chord (not a II chord) because it is minor.
Since it would be inconvenient to always show the individual scale degrees that make up a chord, we’ll often use a simple “block” representation for chords, as shown below.
The color of the block reminds you of the scale degree that the chord is built on. For example, I chords are built off the first scale degree so they have a red block. In addition, the Roman numeral name of the c hord is inside the box. Notice that the ii chord block, for example, is the same for two different arrangements of scale degrees 2, 4, and 6. That is because any combination of scale degrees 2, 4, and 6 create a ii chord as long as scale degree 2 is the lowest note.
The other five basic chords are built just like the I and ii chords so it’s not necessary to go through each one individually. The next example shows the scale degrees that make up each of the seven basic chords and the Roman numeral “block” notation for each chord.
The IV chord, for example, contains scale degrees 4, 6, and 1; the V chord contains scale degrees 5, 7, and 2. Notice that of the seven possible basic chords, three have a major quality indicated by an upper-case Roman numeral (I, IV, and V), and three have a minor quality indicated by a lower-case Roman numeral (ii, iii, and vi). The last chord, vii°, is neither major nor minor; its quality is called diminished (represented by lower case numeral with a degree sign next to it). The vii° chord, however, is not as common in popular music so it will be treated later.
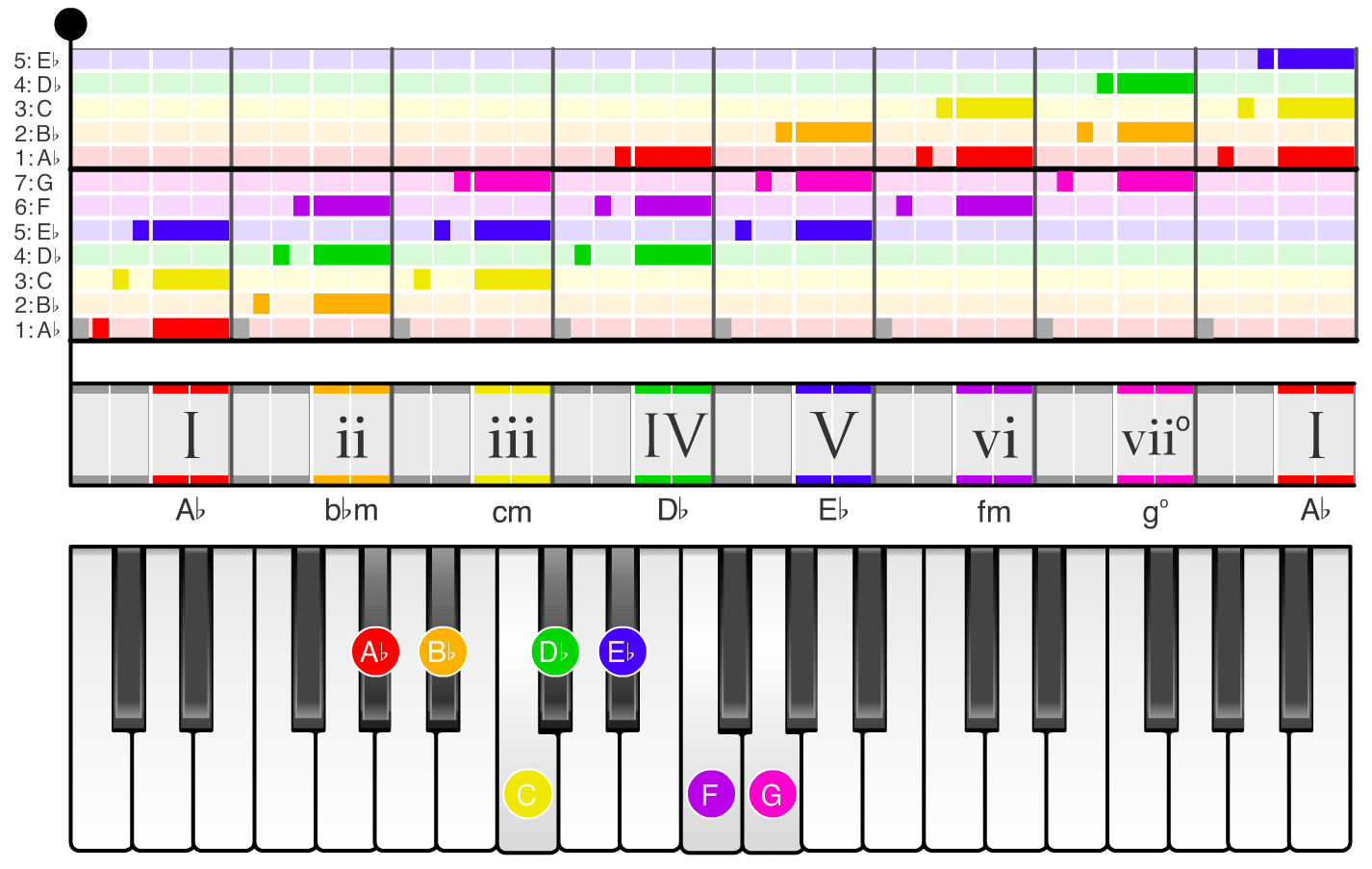
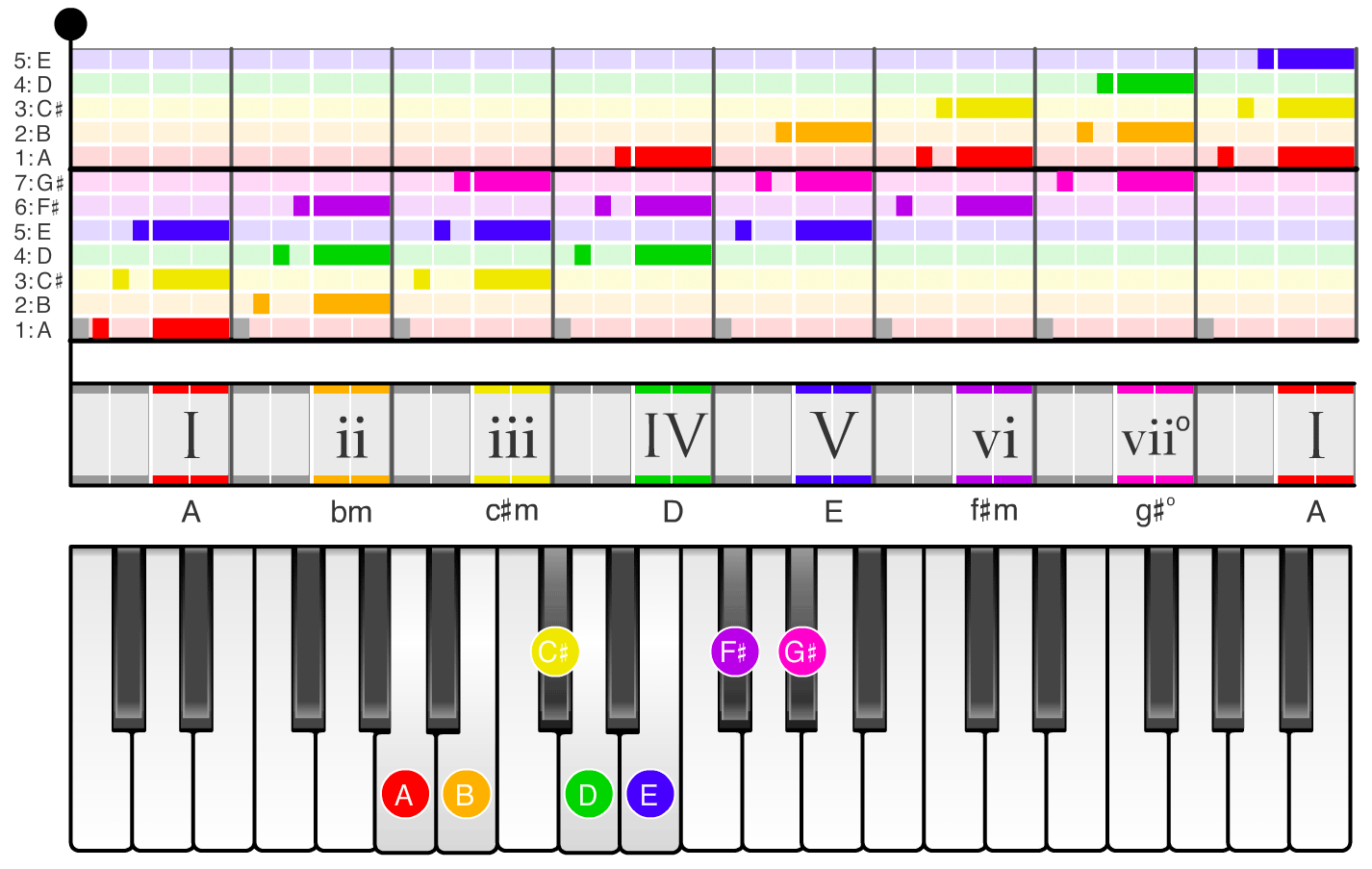
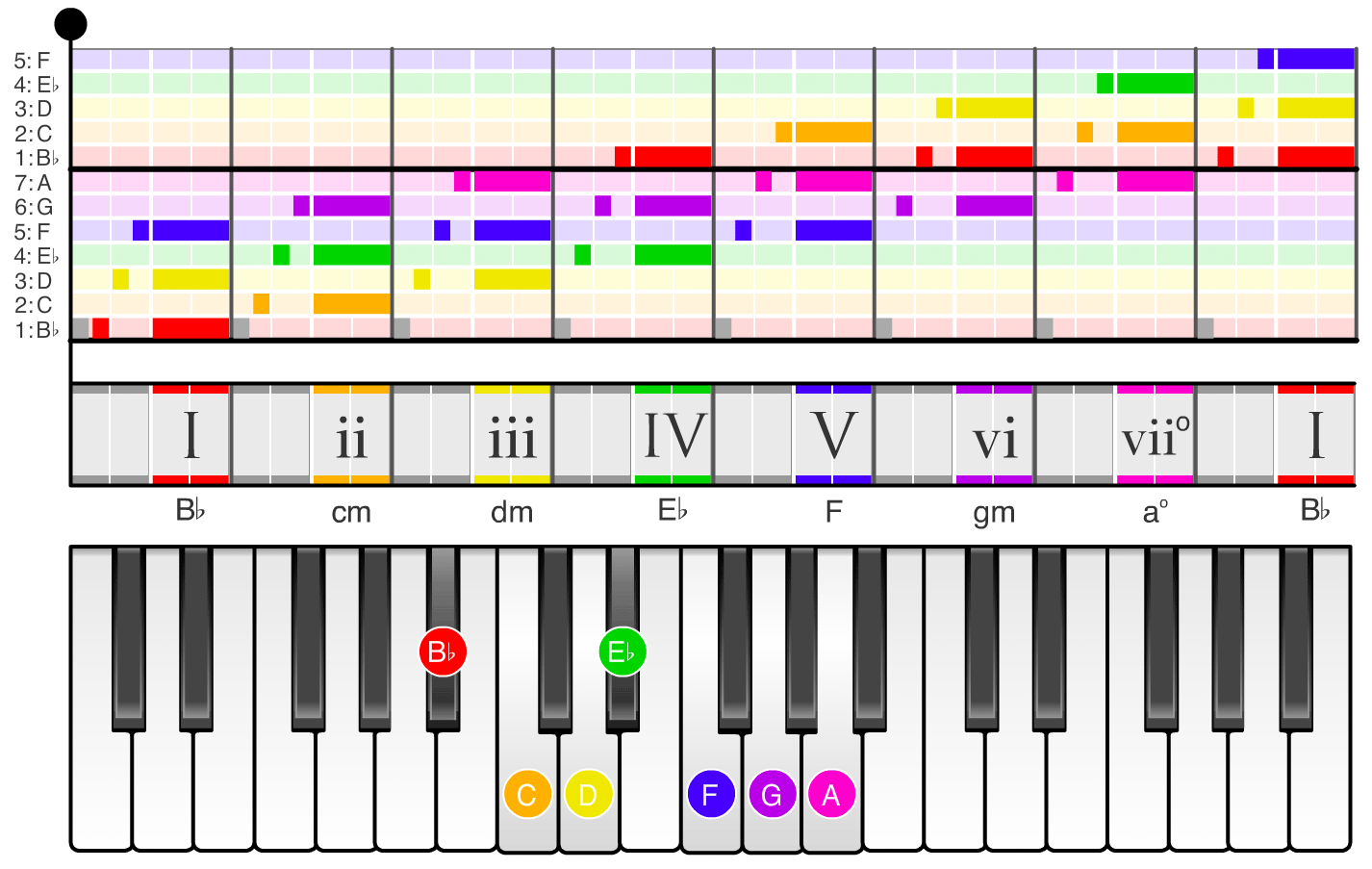
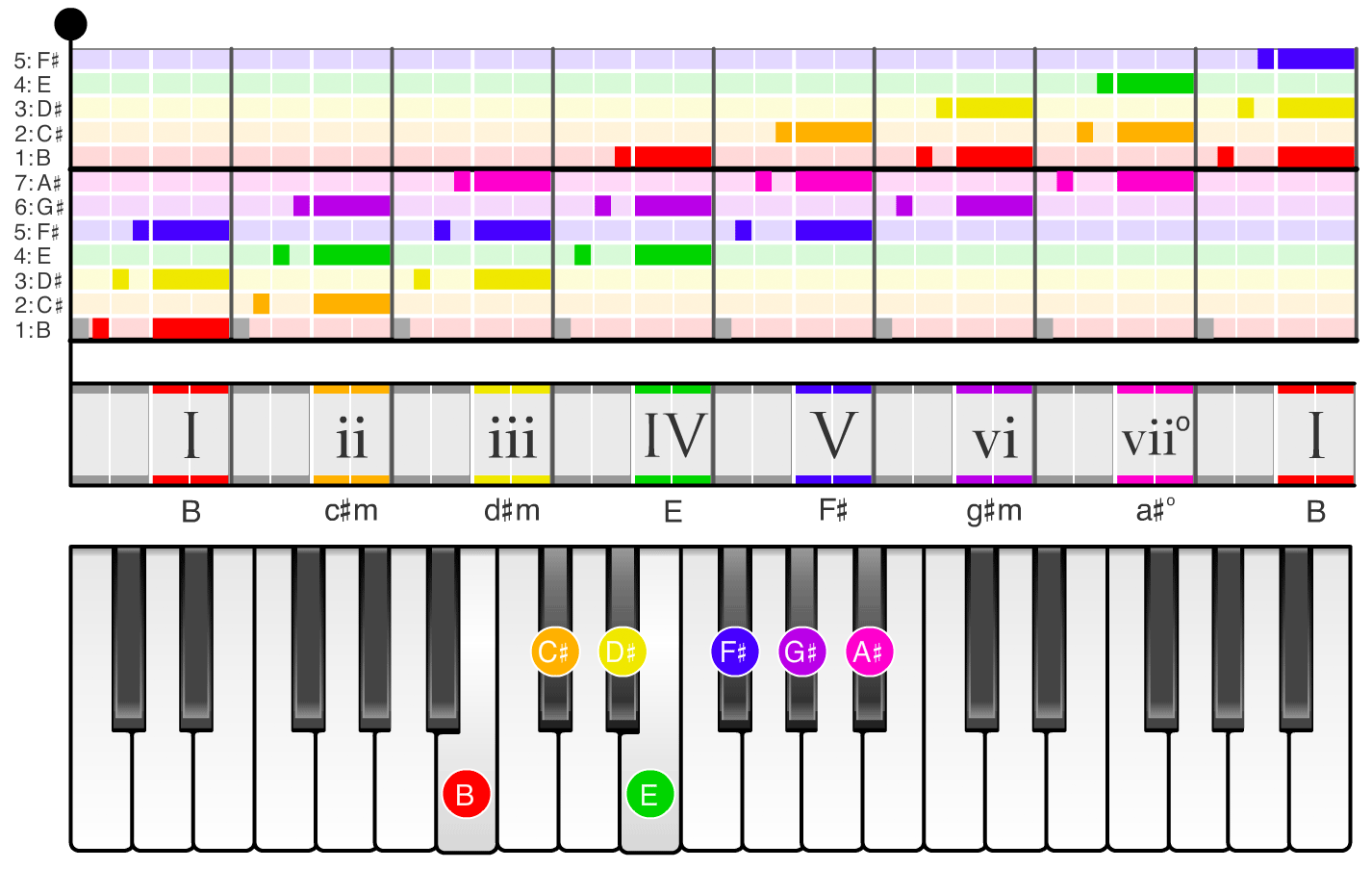
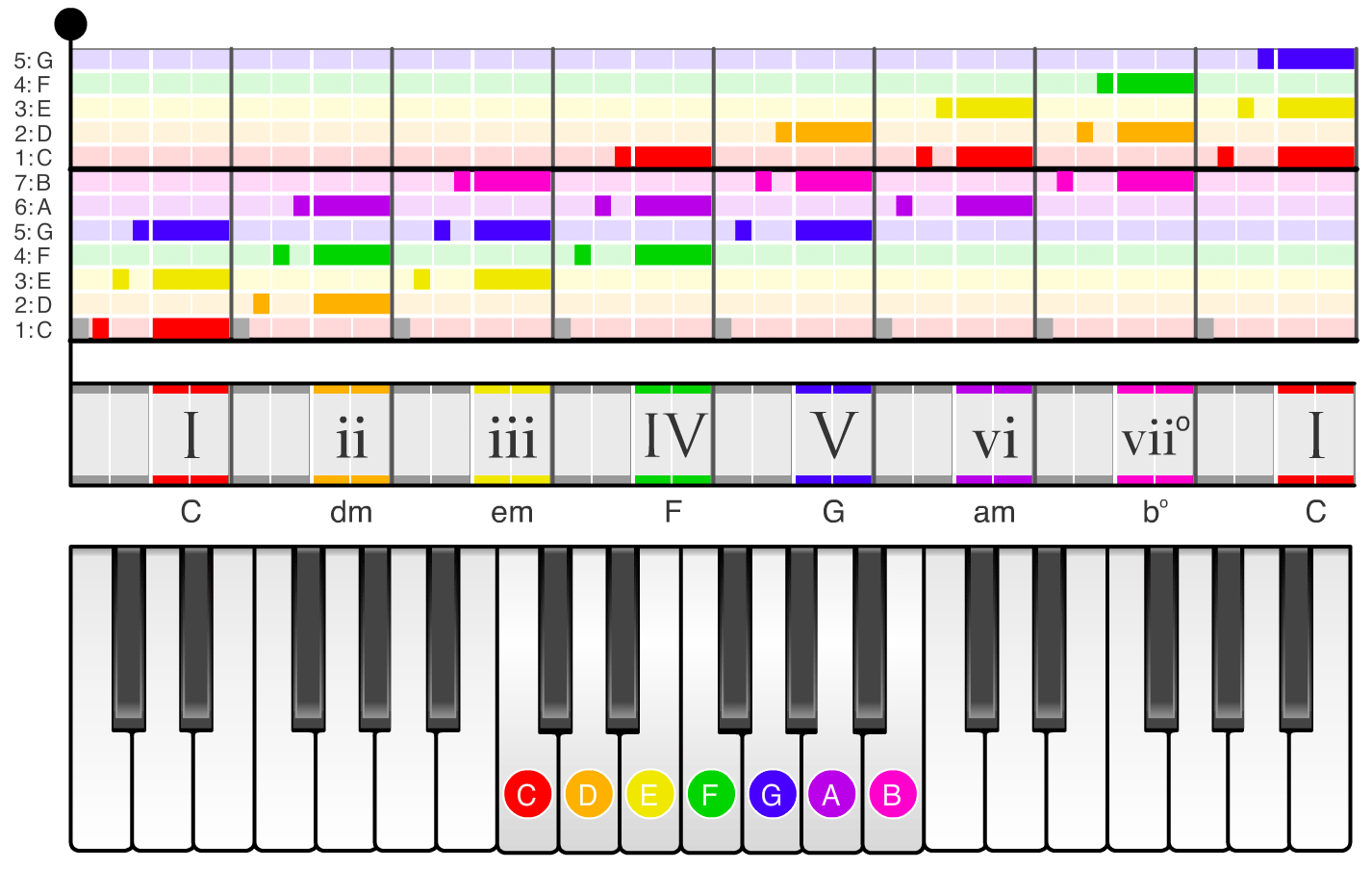
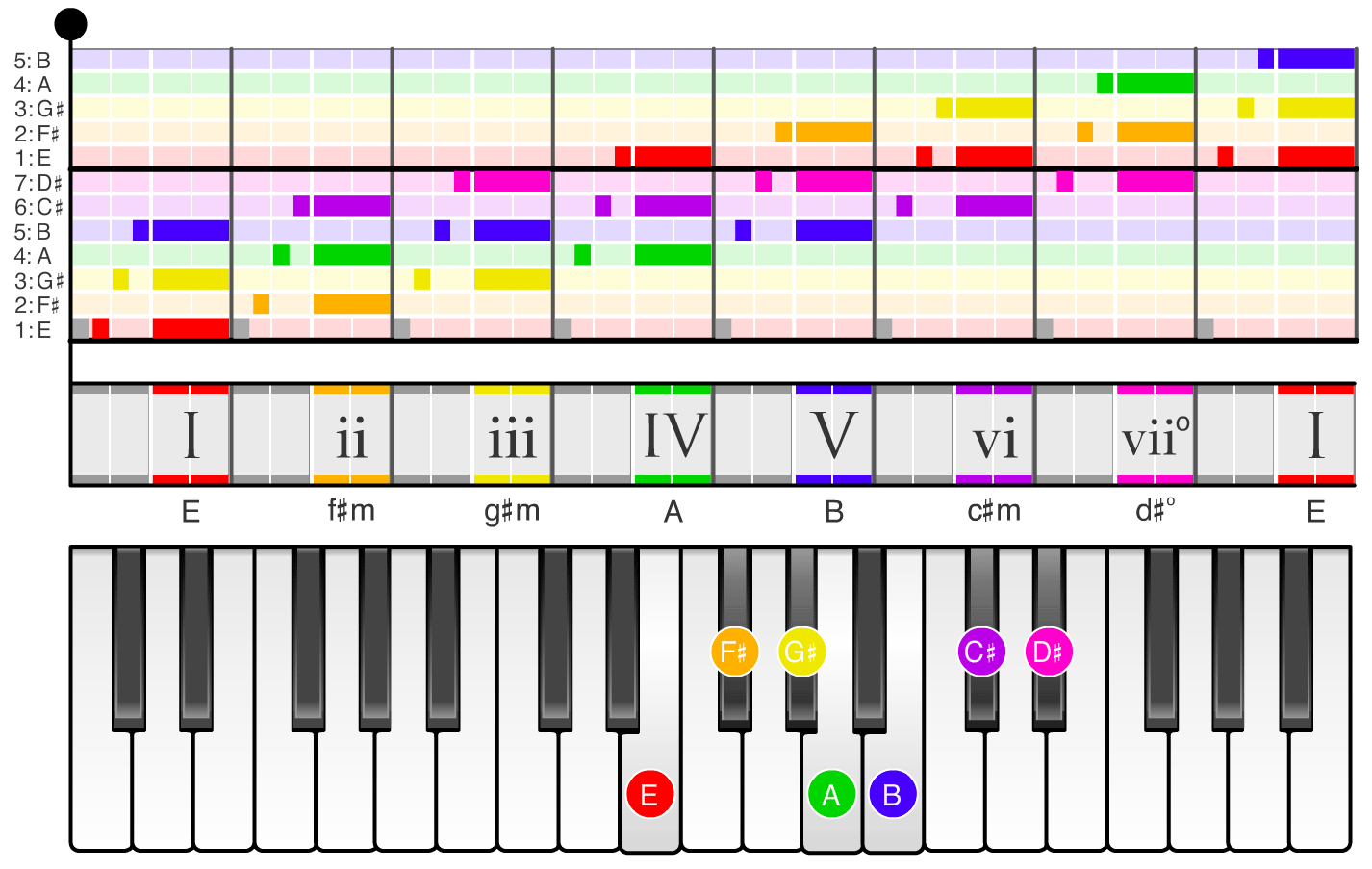
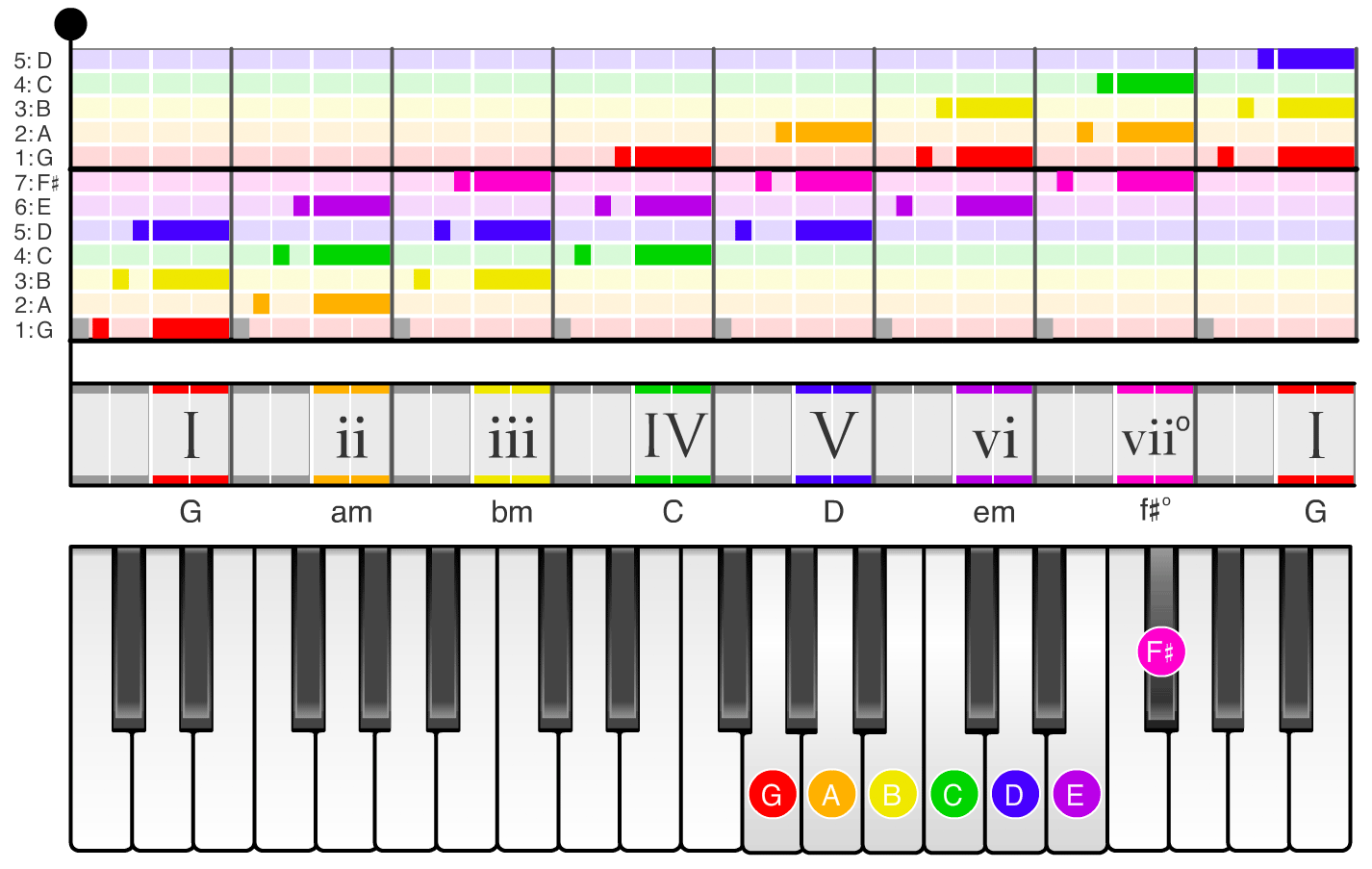
If you swipe through the images in the carousel below, you can see the names of the scale degrees (1, 2, 3, ...) and chords (I, ii, iii, ...) in each of the twelve keys. For example, if you swipe to the the A major scale (the second image in the carousel), the chord names change to A, bm, c#m, D, ... and the notes on the piano shift so the scale starts on the note A. If you swipe to the the D major scale (the sixth image in the carousel), the chord names change to D, em, f#m, G, ... and the notes on the piano shift so the scale starts on the note D.
Songs are constructed by playing a series of chords one at a time in sequence. Sequences of chords are called chord progressions, and many of the later parts of this book will explore how chords within a chord progression are chosen to make a pleasing sound. An example of a chord progression is shown below. Click play to hear how it sounds:
To reinforce the connection between the block representation and the scale degrees it represents, the next example shows the implied arrangement of scale degrees on the relative staff. Notice that in most of the chords, some of the scale degrees are played more than once.
The chord progression you just heard is starting to sound like music, but it really needs a melody to sound complete. In a previous section, we showed you the melody to “Livin’ On A Prayer” by Bon Jovi (it had scale degrees 1-1-1-7-6-5-3-4-4). The next example adds this melody to the chord progression you just heard. Click play to hear how it sounds:
This generic reproduction of “Livin’ On A Prayer” by Bon Jovi shows that the raw chords and melody capture much of what makes a song recognizable. Even though the example uses a generic arrangement for the chords, the chords and melody are immediately recognizable as “Livin’ On A Prayer” (assuming, of course, that you know the song). That’s because underneath all of the sparkle and shine, it’s the basic building blocks of a song that give it its overall character: its chords and melody.
To recap: most popular music can be reduced to just two basic building blocks: the melody, which can be represented by just seven different scale degrees played in some sequence; and the chords, which can be represented by just seven different Roman numerals played in some sequence.
The goal of this book is to teach you the rules and structure behind chord progressions, melody, and their relationship to one another, so you can understand the how and the why behind it all and hopefully apply it to your own playing or songwriting endeavors.
Before we begin, there’s one last thing you should know: while this discussion has been centered around “popular” music, know that much of classical music is governed by the same principles. If classical music is your thing, the topics we cover in this book will go a long way to helping you understand how classical music is structured as well.
Below is a short passage playing the raw chords and melody from Mozart’s famous “Eine Kleine Nachtmusik” shown in relative notation.
Even though Mozart was a master at arranging a room full of instruments to play many different notes in unison, it can all be broken down to the same simple melody and chord components that we’ve been talking about (in this case the entire ensemble has been reduced to just two chords: I and V!)
This is the end of the first chapter of Hooktheory I. To continue on Hooktheory II's chapter 1.2, click the button below.
Continue on 1.2: Qualities of Seventh Chords